Half Space Culling

So far we've rendered everything, no matter what. And that's ok, for small demos. But even the simplest game could not get away from that. Think of a modern game, like Assasins Creed. They have MILLIONS of objects per scene. Rendering them all would make the game unplayable.

So what's the solution? Don't render what you can't see! This is called view culling. We cull out all invisible objects, and NEVER actually render them. Over the years view culling has gotten increasingly more complex, but we're going to start off with the simplest implementation, half space culling.

The theory behind half space culling is simple. Construct a plane at the position of the camera, the plane will span the cameras X and Y axis, and will face in the direction of it's Z axis. Then, test all models we are rendering against this plane. Only render models that are in front of the plane. This way, we don't render anything behind the camera!

How do we actually test what side of the plane a point is on? Using the game programmers bread and butter, the dot product! If you want to google how to do this, you should be looking for Half Space Test.

Plane

A plane in 3D space can be thought of as a flat surface extending indefinitely in all directions. It can be described in several different ways. For examply by:

Three points not on a straight line
A normal, and a point on the plane
A normal, and a distance from origin

Let's define a plane class in code:

class Plane {
  public Vector3 n; // Plane normal. Points x on the plane satisfy Dot(n, x) = d
  public float d; // Distance from origin, d = Dot(n, p), for a given point p on the plane
}

So we've chosen to represent a plane as a normal and a distance from origin. We can calulate this plane, from 3 (3D) points

static Plane ComputePlane(Vector3 a, Vector3 b, Vector3 c) {
  Plane p = new Plane();
  p.n = Vector3.Normalize(Vector3.Cross(b - a, c - a));
  p.d = Dot(p.n, a);
  return p;
}

When two planes are not parallel to each other, they intersect in a line. Similarly, three planes (two not parallel to each other) intersect at a 3D point.

Theory

The theory of a half space test is simple. Given a plane, with a normal. What is the angle between the plane and the point!

Remember how the dot product works! If we take the planes up vector, and a vector from the plane to the point we are testing we can do a dot product between the two vectors.

The result of this dot product is the half space test, remember if the result of the dot product is:

0, the vectors are perpendicular (90 degrees)
positive, the vectors are less than 90 degrees apart
negative, the vectors are more than 90 degrees apart

So, if the dot product of the planes vector and the vector from the plane to the point is:

0, the point is on the plane
positive, the point is in front of the plane
negative, the point is behind the plane

Half Space Test

Before we talk about the half space test, let's take a quick look at the plane equasion (Equasion of a plane).

a * x + b * y + c * z + d = 0

Where, ABC is the normal of the plane, D is the distance of the plane from origin and XYZ is some point. This equasion states that if point XYZ is on the plane, the result of the above equasion is 0. If a point is in front of the plane the result will be a positive number (distance from the plane) and if the point is behind the plane the result will be a negative number.

Because you already know what ABC and D are, you could just plug int XYZ into the above equasion and return the result. Try implementing this function in code

static float HalfSpace(Plane p, Vector3 v) {
  // TODO: Return result of plane equasion
}

The above code is the preffered method of implementing the half space test. A solution is given at the end of the page

Alternate representation

There are other ways of representing planes, and doing the half space test. For example, a plane can be represented by a normal and any point on the plane. As opposed to what we have now, a normal and a distance from origin.

If this was the case, the half space test would in involve subtracting the plane point from the point you are testing to get a direction vector, then doing a dot product with the plane normal and direction vector.

Because the dot product returns a number that is relative to an angle this representation might be easyer to understand.

If the dot of the plane normal and direction vector is negative, then the angle is greater than 90 degrees
if it is 0 then the angle is exactly 90 degrees (on the plane)
If it is positive, then the angle is less than 90 degrees

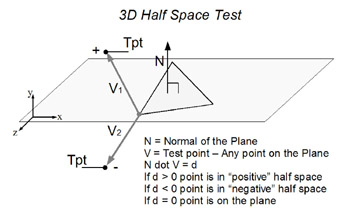
We can actually make a point on the plane by multiplying the plane normal by the plane distance. Once we have a point on the plane we could use the dot product to perform a half space test.

public static float HalfSpace(Plane p,Vector3 v) {
    Vector4 N = new Vector4(p.n.X, p.n.Y, p.n.Z, 0f);
    Vector4 PointOnPlane = new Vector4(p.n.X * p.d, p.n.Y * p.d, p.n.Z * p.d, 1);
    Vector4 V = PointOnPlane - new Vector4(v.X, v.Y, v.Z, 1f);
    return Vector4.Dot(N, V);
}

Implementation

Cool, now that we understand the half space test (If you don't call me on skype) let's go ahead and implement it in our test scene.

Implement a Plane class, and the HalfSpace function. For ease of use, make the HalfSpace function a static member of the Plane class. Also, make the ComputePlane function a static member of the plane class.

Inside the example application, after all the camera variables, add a new Plane variable:

... old code
protected Vector3 CameraPosition = new Vector3(0, 0, 10);
protected Vector2 LastMousePosition = new Vector2();
protected Matrix4 viewMatrix;
// NEW
Plane cameraPlane = null;

We're going to construct this new plane inside the Move3DCamera function. We know we can construct a plane using 3 points, so what 3 points of the camera can we use to make a plane?

Well we know the forward and right and up of the camera. We can use the right and up to construct a camera plane whose normal will be the camera forward. But that's only two vectors, what about the third one? We can invert the right vector to get a left vector.

This means we can create the camera plane using the camera world matrix left, right and up planes. Let's see how this would look in code:

...old code
Matrix4 position = Matrix4.Translate(CameraPosition);
Matrix4 cameraWorldPosition = orientation * position;
Matrix4 cameraViewMatrix = Matrix4.Inverse(cameraWorldPosition);

// NEW
right = new Vector3(cameraWorldPosition[0, 0], cameraWorldPosition[1, 0], cameraWorldPosition[2, 0]);
Vector3 left = new Vector3(-right.X, -right.Y, -right.Z);
Vector3 up = new Vector3(cameraWorldPosition[0, 1], cameraWorldPosition[1, 1], cameraWorldPosition[2, 1]);

right = Matrix4.MultiplyPoint(cameraWorldPosition, right);
left = Matrix4.MultiplyPoint(cameraWorldPosition, left);
up = Matrix4.MultiplyPoint(cameraWorldPosition, up);

cameraPlane = Plane.ComputePlane(left, right, up);

// OLD
return cameraViewMatrix;
... old code

We get the right, and up out of the matrix, then invert right to get left. Remember, you can extract a matrices forward, right and up basis vectors because they make up the upper 3x3 matrix:

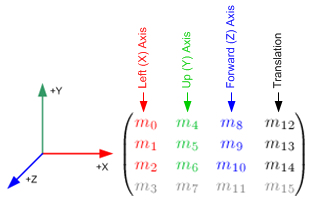
We could have multiplied the right and up vectors by the orientation matrix, like earlyer in this same function, but extracting the vectors straight from the matrix is much simpler (and a lot less expensive). And you should be aware of both ways to extract the vector.

However, extracting these vectors is not enough. These are vectors, not points, so the translation has not been applied yet. That's why we multiply each of these vectors by the world matrix of the camera.

After we have left, right and up in world space (each one unit away from the cameras position), we can construct the camera plane.

Finally, lets modify the render code:

if (Plane.HalfSpace(cameraPlane, new Vector3(0f, 0f, 0f)) >= 0) {
    GL.Color3(1f, 1f, 1f);
    model.Render(true, false);
}
else {
    Console.WriteLine("Green susane culled");
}

Now if you move past susane, or rotate the camera that she's off screen, we wont see her. But some text will be written to the console instead.

Why are we testing 0, 0, 0 for susane, because she is rendered at origin. If you have a model rendered at 2, 4, 6 you would test that point.

Solution

Above i mentioned a solution would be given at the end of the page:

static float HalfSpace(Plane p, Vector3 v) {
  return (p.n.X*v.X) + (p.n.Y*v.Y) + (p.n.Z*v.Z) + p.d;
}

Halfspace Culling