The missing functions

One of the nice things about being able to use your own matrices in OpenGL is having to rely less on the OpenGL functions. After all, you don't really know what those functions are doing under the hood! If we want to fully break away from OpenGL we have timplement 3 more functions into our Matrix4 class: Ortho, Frustum and LookAt.

Make these changes in the Math Implementation repository, once they are working, copy the Matrix4.cs file into your OpenGL1X repository, replacing the old file.

All three of these functions are going to be static! They don't modify any existing matrix, just return a new matrix specifying some sort of transformtaion!

Deriving matrices is hard. I honestly have no idea how to derive an Orthographic projection matrix. What i will preset below is the formulas i've memorized and the things that work for me. If you want to be mathematically accurate, this tutorial is a decent walktrough of how to derive the matrices. It's not a skill you will ever need, i've never used it once.

Ortho

How OpenGL makes an orthographic matrix is not a secret. It's actually outlined in the OpenGL specification. Use the following image to create your own Matrix4.Ortho function:

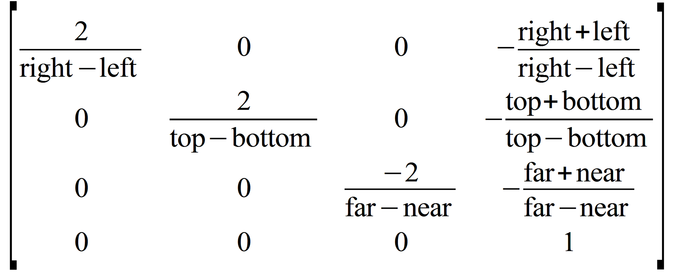
You can test this by changing the projection fo Mr.Roboto from the perspective projection to:

float aspect = (float)MainGameWindow.Window.Width / (float)MainGameWindow.Window.Height;
GL.Ortho(-25.0f * aspect, 25.0f * aspect, -25.0f, 25.0f, -25.0f, 25.0f);

Take not of what it looks like, then replace the GL.Ortho call with your own matrix:

float aspect = (float)MainGameWindow.Window.Width / (float)MainGameWindow.Window.Height;
Matrix4 ortho = Matrix4.Ortho(-25.0f * aspect, 25.0f * aspect, -25.0f, 25.0f, -25.0f, 25.0f);
GL.LoadMatrix(Matrix4.Transpose(ortho).Matrix);

The two screens should look the same.

Frustum

Re-implementing OpenGL's Frustum function is not too difficult either, as the math behind it is toroughly documented. This matrix is one of the few matrices who's element [3,3] is not 1.

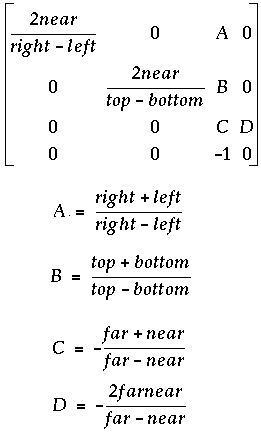
The formula is available as text on the OpenGL man page. I know D is a bit hard to read it's D = -((2 * far * near) / (far - near))

You can test if your function is correct, by changing the Mr.Roboto sample back to using it's original projection matrix. Then replace the Perspective function with one that uses your frustum instead of the built in one:

public static void Perspective(float fov, float aspectRatio, float zNear, float zFar) {
    float yMax = zNear * (float)Math.Tan(fov * (Math.PI / 360.0f));
    float xMax = yMax * aspectRatio;

    //GL.Frustum(-xMax, xMax, -yMax, yMax, zNear, zFar);
    Matrix4 frustum = Matrix4.Frusum(-xMax, xMax, -yMax, yMax, zNear, zFar);
    GL.MultMatrix(Matrix4.Transpose(frustum).Matrix);
}

Look At

LookAt is an interesting beast, as it is not a part of the OpenGL specification. It's not really a part of OpenGL. The LookAt function was made popular by a library called GLU (GL Utilities).

I'm going to walk you trough creating the LookAt function step by step both the theory and the code.

We start with the funtion signature. We've already discussed what these arguments do, i won't discuss them here.

 public static Matrix4 LookAt(Vector3 position, Vector3 target, Vector3 worldUp) {

We can create a vector from the camera to the target by subtracting position from target (to get a vector pointing from position to target. If we normalize this vector to have a magnitude of 1 it becomes the forward basis (z) vector for the cameras coordinate system.

    Vector3 cameraForward = Vector3.Normalize(target - position);

Remember when you cross two vectors the result is a vector that's perpendicular to both. We can cross the world up vector with the cameras forward to get a vector to the right side of the camera. If we normalize this vector, the result will be our right basis (x) vector.

    Vector3 cameraRight = Vector3.Normalize(Vector3.Cross(cameraForward, worldUp));

Now that we know the up and the right vector of the camera's coordinate system we need to figure out it's up vector. The up is going to be perpendicular to forward and right, so we simply take their cross products. Because both matrices are normalized, we don't need to normalize this.

    Vector3 cameraUp = Vector3.Cross(cameraRight, cameraForward);

Now that we have all 3 basis vectors that make up the cameras coordinate system, let's combine them into a matrix! Remember, in OpenGL -z is forward, so we have to negate our foward vector.

    Matrix4 rot = new Matrix4(cameraRight.X, cameraUp.X, -cameraForward.X, 0.0f,
                              cameraRight.Y, cameraUp.Y, -cameraForward.Y, 0.0f,
                              cameraRight.Z, cameraUp.Z, -cameraForward.Z, 0.0f,
                              0.0f, 0.0f, 0.0f, 1.0f);

That takes care of the rotation, but the camera has a position in the world too! Let's create a translation matrix for it:

    Matrix4 trans = Matrix4.Translate(position);

Now it goes to reason the camera matrix will be rot * trans. But remember, the view matrix is the inverse of the camera matrix. So we must invert these matrices before returning them:

    return Matrix4.Inverse(rot) * Matrix3.Inverse(trans);
}

And thats it! You now have a working LookAt function! Make sure it works by replacing the existing LookAt in MR.Roboto with yours, like so:

GL.MatrixMode(MatrixMode.Modelview);
GL.LoadIdentity();
//LookAt(10.0f, 5.0f, 15.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f);
Matrix4 lookAt = Matrix4.LookAt(
    new Vector3(10.0f, 5.0f, 15.0f),
    new Vector3(0.0f, 0.0f, 0.0f),
    new Vector3(0.0f, 1.0f, 0.0f)
);
GL.MultMatrix(Matrix4.Transpose(lookAt).Matrix);

Faster LookAT

By far the most improtant part of our LookAT function is this line:

return Matrix4.Inverse(rot) * Matrix3.Inverse(trans);

Doing one matrix inverse is pretty expensive. Doing two is worse! We know that a translation matrix looks like this:

1, 0, 0, Tx
0, 1, 0, Ty
0, 0, 1, Tz
0, 0, 0, 1

We also know that it's inverse simply looks like this:

1, 0, 0, -Tx
0, 1, 0, -Ty
0, 0, 1, -Tz
0, 0, 0, 1

So it stands to reason that we can speed this up, if instead of inverting the translation matrix we build it using the inverse of the position vector:

Matrix4 trans = Matrix4.Translate(position * -1.0f);
return Matrix4.Inverse(rot) * trans;

Hey that's awesome! If we run the game with this look at function everything looks the same. Now, the big question is, can we somehow get rid of that other Inverse? Surprisingly the answer is yes.

The rot matrix we have above is VERY special. It's what we call an ortho-normal matrix. An ortho normal matrix is a matrix who's basis vectors are perpendicular to each other, and are all of unit length. Our rot matrix meets this criteria.

Now for the special part. If an ortho-normal matrix has NO TRANSLATION (which the rot matrix does not), it's inverse is the same as it's transpose! Crazy! This is super special case and works in only a few specific instance. This is one of those instances. This means we can rewrite the last two lines as:

Matrix4 trans = Matrix4.Translate(position * -1.0f);
return trans * Matrix4.Transpose(rot);

And now we have no Inverse functions in the LookAt function at all!

Conveniance getter

Having to type out

Matrix4.Transpose(frustum).Matrix

every time we want to use one of our custom matrices with OpenGL is very time consuming. We can save a LOT of time by adding a simple getter to the matrix class that returns the matrix as a transposed array of floating point numbers. How OpenGL is expecting it:

public float OpenGL {
    get {
        return Transpose(this).Matrix;
    }
}

There, much nicer. Now if i want to load my own matrix, i just have to:

Matrix4 frustum = Matrix4.Frusum(-xMax, xMax, -yMax, yMax, zNear, zFar);
GL.MultMatrix(frustum.OpenGL);

Conveniance perspective:

We now have a Frustum function in our Matrix class. But to set a Perspective projection we still call the Projection helper function. Now that we know how a frusum matrix is made, and we know the math of Projection, why don't we just make a function in Matrix4 that returns a straight up projection and makes it so we don't have to mess with any helper functions?

Let's go ahead and do that. All you really have to do is to move the Perspective helper into the matrix class, and return the final matrix.

You know the drill, test it out by replacing the old function.

Projection & LookAt