Custom Matrices
Using OpenGL matrix functions is pretty easy. And the stack makes working with matrices even easyer. But you already have a Matrix class built. Which already offers everything OpenGL matrices offer, and more!
Tour matrices are also a bit easyer to work with than OpenGL's because you have full control and know they are mathematically accurate. Wouldn't it be great if you could use your own matrices to work with OpenGL?
Good news, you can!
OpenGL Matrix
The OpenGL matrix has been confusing programmers since 1992. This next bit might get a bit confusing. So, bear with me; re-read the section if you need to and call me on Skype if you have questions.
Mathematically OpenGL uses column major matrices. Because the matrices are column major, OpenGL uses column vectors. This means OpenGL works post multiplication because a vector is a 4x1 matrix, so in order for inner dimensions to match it has to go on the right hand side of a matrix. matrix * vector. The matrices are right handed, that is -Z is forward, it goes into the monitor.
Everything bolded in the above paragraph is the theoretical law of the land in OpenGL world. Write them on a notecard, memorize them! That is how the OpenGL specification says OpenGL matrices will work.
A column major matrix has it's basis vectors in the first 3 columns and it's translation vector in the 4th column, like so:
Xx Yx Zx Tx
Xy Yy Zy Ty
Xz Yz Zz Tz
0 0 0 1
Topology
Topology refers to how the matrix is stored in memory, THIS is where OpenGL gets confusing. Consider the following column major matrix:
Xx Yx Zx Tx
Xy Yy Zy Ty
Xz Yz Zz Tz
0 0 0 1
Given that a matrix is stored as an array of floats (size 16) you would expect it to be laid out in memory like so:
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]
Xx Yx Zx Tx Xy Yy Zy Ty Xz Yz Zz Tz 0 0 0 1
Which makes sense, the matrix is stored 1 row at a time in a linear array. The X basis vector occupies elements 0, 4, 8 and 12. This is how your matrix works, and to be honest; this is how any sane persons matrix would be written.
In the above example, the matrix is stored linearly one row at a time.
Not OpenGL
In OpenGL the following (still column major) matrix:
Xx Yx Zx Tx
Xy Yy Zy Ty
Xz Yz Zz Tz
0 0 0 1
Is stored in memory like this:
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]
Xx Xy Xz 0 Yx Yy Yz 0 Zx Zy Zz 0 Tx Ty Tz 1
That is, the matrix is stored one column at a time. Instead of storing each row in memory one after another, OpenGL stores each column in memory, one after another.
This is actually a very un-intuitive way to store a matrix. So, why does OpenGL do it this way? When the standard for the OpenGL Matrix was defined in 1992 the hardware of the time could run three times faster with this memory layout. Today it's a neusance, a major source of confusion and annoyment. But we have to keep doing things this way for historical reasons.
Take a few minutes, let that sink in. See if you can figure out how the following matrix would be stored in OpenGL's memory and in your matrices memory. Keep in mind, the matrix is stored in a 1 dimensional float array that has 16 elements. Let me know on skype before moving on to the next section:
A B C D
E F G H
I G K L
M N O P
Transpose
The takeaway from the above section is actually rather simple, while you use the same theoretical memory layout as OpenGL (column major, post multiplication) you actually store your data in memory transposed of how OpenGL store it's data in memory.
This just means that before you load your own custom matrix into OpenGL, you must transpose it.
Loading a matrix
Now with all that theory out of the way, how do you actually load a matrix into OpenGL? There are two functions, the first one isGL.LoadMatrix. This function takes an array of float's as an argument:
void GL.LoadMatrix(float[] matrix);
This function will take the matrix passed into it, and REPLACE whatever is on the top of the stack with the matrix. It's useful for loading the view matrix, but after that you can't really use it for much else without ruining the view matrix.
The second method is GL.MulMatrix, like LoadMatrix it takes an array of 16 floats:
void GL.MulMatrix(float[] matrix);
Unlike LoadMatrix, MulMatrix respects the top of the stack. It's going to take whatever argument you give it and multiply the top of the matrix stack by that argument. This is the function you wan to use to load custom matrices onto an existing stack
Sample
Let's see how to use it. Make a new demo scene that extends the Game class. We will need the LookAt, Perspective and DrawCube functions. Also include a grid.
Draw a cube at 1, 0, 0; rotated 45 degrees on the x axis; with a scale of 0.5f.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using OpenTK.Graphics.OpenGL;
namespace GameApplication {
class MatrixDemo1 : Game {
Grid grid = null;
public override void Initialize() {
grid = new Grid();
}
protected static void LookAt(float eyeX, float eyeY, float eyeZ, float targetX, float targetY, float targetZ, float upX, float upY, float upZ) {
// Copy / paste
}
public static void Perspective(float fov, float aspectRatio, float znear, float zfar) {
// Copy / paste
}
public static void DrawCube() {
// Copy / paste
}
public override void Render() {
GL.Viewport(0, 0, MainGameWindow.Window.Width, MainGameWindow.Window.Height);
GL.MatrixMode(MatrixMode.Projection);
GL.LoadIdentity();
Perspective(60.0f, (float)MainGameWindow.Window.Width / (float)MainGameWindow.Window.Height, 0.01f, 1000.0f);
GL.MatrixMode(MatrixMode.Modelview);
GL.LoadIdentity();
LookAt(
10.0f, 4.0f, 0,
0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f
);
grid.Render();
GL.PushMatrix();
GL.Color3(1.0f, 0.0f, 0.0f);
GL.Translate(-2, 1, 3);
GL.Rotate(45.0f, 1.0f, 0.0f, 0.0f);
GL.Scale(0.5f, 0.5f, 0.5f);
DrawCube();
GL.PopMatrix();
}
}
}
Here is what this screen looks like:
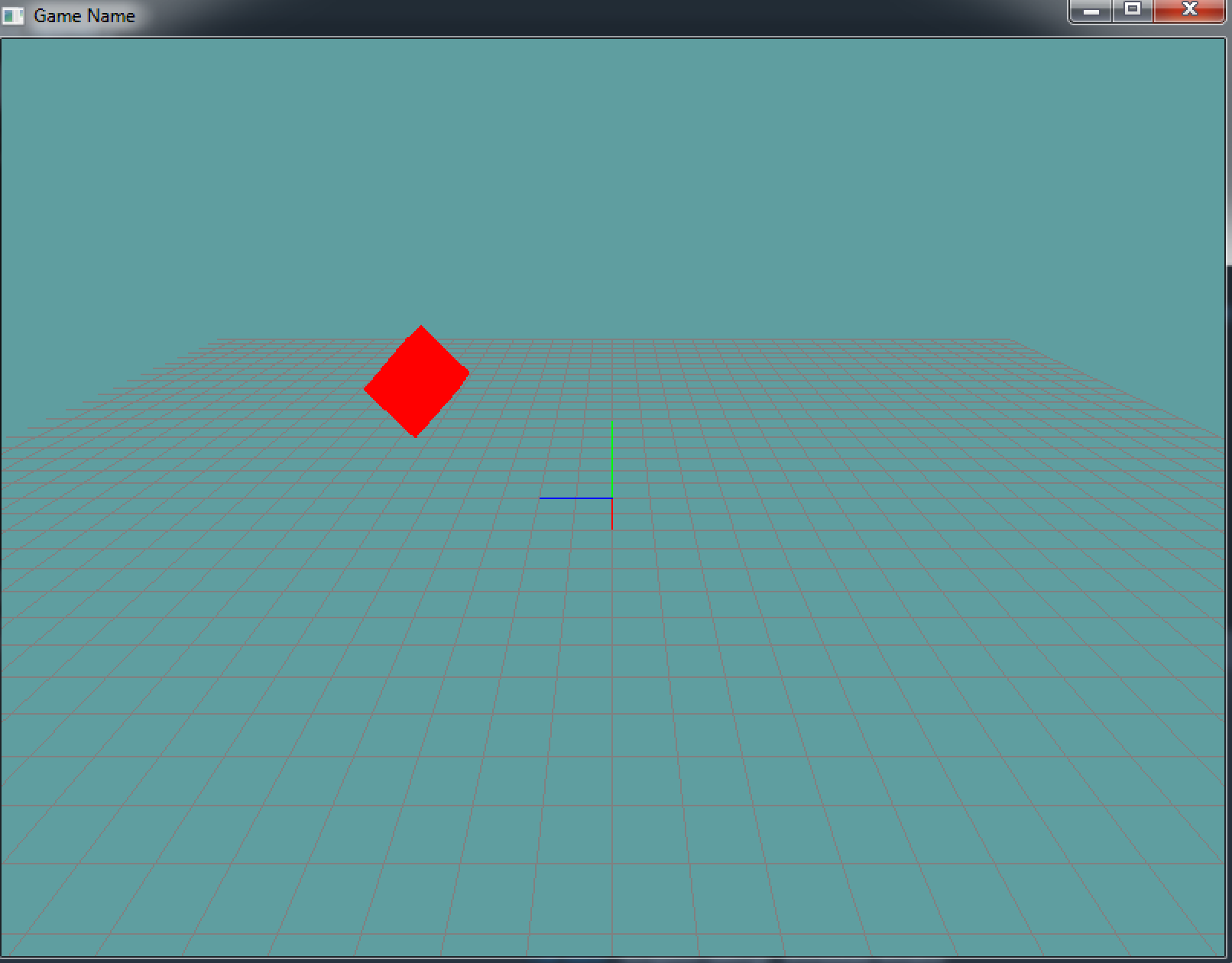
Let's see if we can replace the model matrix of the rendered cube with our own custom matrix.
Check Math Implementation on github, i opened a new ticket. Fix it before moving on! When you're using custom matrices and things don't render correctly (but they did with OpenGL matrices) the problem is always with your implementation. Even if it passed a few unit tests, the real word scenario sometimes breaks down.
First thing's first, import your math implementation code into the project. Keep things clean, put those files under a folder in visual studios solution view. I'd also like you to put your demo scenes in their own folder, like this:
Make sure to use the namespace these where implemented under using Math_Implementation;. The namespace OpenGK also contains a Matrix4 class, so make sure you are not using the namespace directly. Meaning this is ok: using OpenTK.Graphics.OpenGL; but don't do this: using OpenTK;.
Replacing the OpenGL matrices.
Let's look at the render funtion with your custom matrices in place:
public override void Render() {
GL.Viewport(0, 0, MainGameWindow.Window.Width, MainGameWindow.Window.Height);
GL.MatrixMode(MatrixMode.Projection);
GL.LoadIdentity();
Perspective(60.0f, (float)MainGameWindow.Window.Width / (float)MainGameWindow.Window.Height, 0.01f, 1000.0f);
GL.MatrixMode(MatrixMode.Modelview);
GL.LoadIdentity();
LookAt(
10.0f, 4.0f, 0,
0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f
);
grid.Render();
GL.Color3(1.0f, 0.0f, 0.0f);
GL.PushMatrix();
{
Matrix4 scale = Matrix4.Scale(new Vector3(0.5f, 0.5f, 0.5f));
Matrix4 rotation = Matrix4.AngleAxis(45.0f, 1.0f, 0.0f, 0.0f);
Matrix4 translation = Matrix4.Translate(new Vector3(-2, 1, 3));
// SRT: scale first, rotate second, translate last!
Matrix4 model = translation * rotation * scale;
// Remember to transpose your matrix!
GL.MultMatrix(Matrix4.Transpose(model).Matrix);
DrawCube();
}
GL.PopMatrix();
}
As you can see we create 3 matrices: scale, rotation and translation. We make the model matrix for the cube by combining the 3 transformation matrices we created. Because we're in column major (post multiplcation) we multiply right to left.
As discussed, we can't apply the matrix directly, because we're storing it in a different manner than OpenGL expects. So, we transpose the matrix before giving it to OpenGL.
We use GL.MulMatrix. When that call is reached the only thing on the stack is the view matrix. GL.MulMatrix will multiply our matrix into the view matrix to create a modelView matrix.
We still need to push and pop matrices. We do this to restore the top of the matrix stack to the view matrix, in case anything else needs to be rendered.
One thing you may have noticed is i put a { } block inside GL.PushMatrix and GL.PopMatrix. Why did i do this?
Well, we made 4 local matrices: scale, rotation, translation and model. Instead of those matrices being scoped to the function, they are now scoped to those brackets. So, if we have two cubes, we can re-use the matrix names as the ones up there fall out of scope when the } is hit.
Like this:
public override void Render() {
// Omitted to save space, everything up to grid.Render is here
GL.Color3(1.0f, 0.0f, 0.0f);
GL.PushMatrix();
{
Matrix4 scale = Matrix4.Scale(new Vector3(0.5f, 0.5f, 0.5f));
Matrix4 rotation = Matrix4.AngleAxis(45.0f, 1.0f, 0.0f, 0.0f);
Matrix4 translation = Matrix4.Translate(new Vector3(-2, 1, 3));
Matrix4 model = translation * rotation * scale;
GL.MultMatrix(Matrix4.Transpose(model).Matrix);
DrawCube();
}
GL.PopMatrix();
GL.Color3(0.0f, 1.0f, 0.0f);
GL.PushMatrix();
{
Matrix4 scale = Matrix4.Scale(new Vector3(0.5f, 0.5f, 0.5f));
Matrix4 rotation = Matrix4.AngleAxis(45.0f, 0.0f, 1.0f, 0.0f);
Matrix4 translation = Matrix4.Translate(new Vector3(5, 3, -4));
Matrix4 model = translation * rotation * scale;
GL.MultMatrix(Matrix4.Transpose(model).Matrix);
DrawCube();
}
GL.PopMatrix();
}
As you can see i can create matrices by the same name, without reusing the old ones because they are scoped to local code blocks denoted by { } pairs.