Ray Against Sphere
Given the following image, we have :
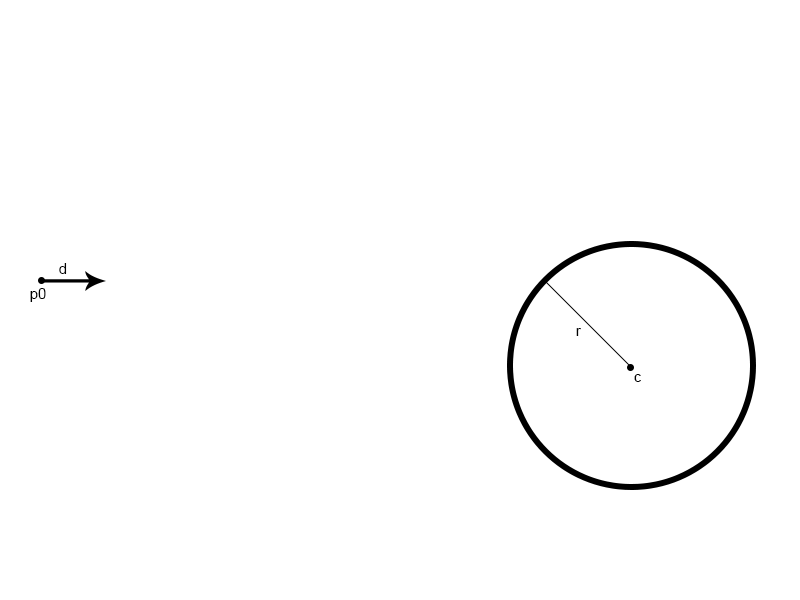
- Ray R, defined by:
- point p0
- normal d
- Sphere S, defined by:
- center point c
- radius r
Given this information, we want to find out if ray R intersects sphere S. If the ray intersects the sphere, it's going to be along the normal. In the image below, t is the length at which the normal intersects the sphere:
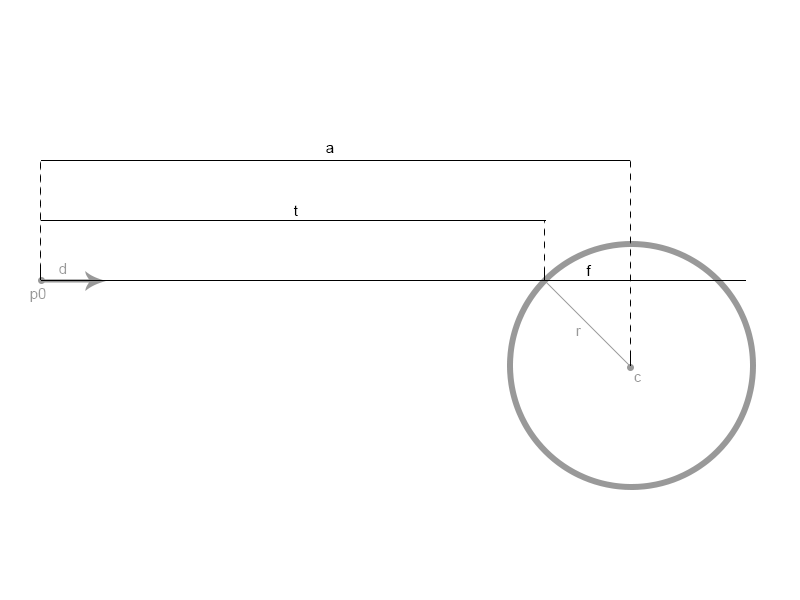
An intersection happens at time t, along ray R. Another way to express this would be that the intersection happens at R(t). To find t, we need to first find a and f. The formula for t is:
t = a - f
In order to find a and f, we need two more vectors, vector e and vector b. Vector e is the vector from p0 to c. Vector b is one side of the right triangle formed by vectors r, f and b. The image below demonstrates this. You know r and f, you have to solve the right triangle for b.
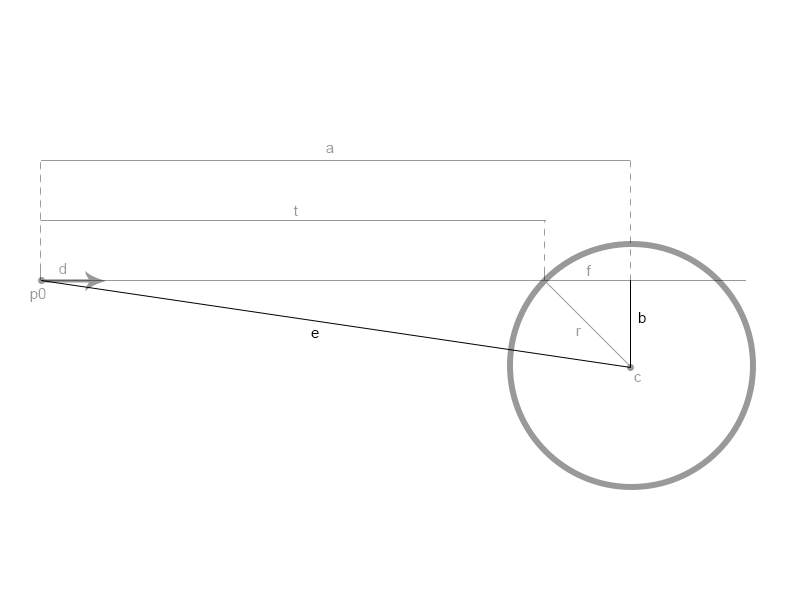
In this image, we have two triangles we care about.
- Triangle f, b, r
- Triangle a, e, b
Given these two triangles, we can figure out the following
- Vector e is a vector going to p0 to c
- Vector a is vector e projected onto vector d
- Vector b is given by the pathegroen therom
- : Therom
- : Triangle a, e, b
- : Re-arranged
- :final
- Vector f is given by the pathegroen therom
- : Triangle f, b, r
- : Re-arranged
- Now we can solve for t
- : algorithm for t
- : Expanded f
- : Expanded b, final
With that, we have the value of t!
What happens when the ray doesn't hit the sphere? The expression inside the square root will be negative. Therefore, we have to make an early out test for that!
There is one more edge case, if is less than the squared radius of the sphere, the ray starts INSIDE the sphere! This is again a special case that we need to handle delicatley.
The Algorithm
In the above diagrams, it's not always clear what is a vector value and what is a scalar value! When a vector is used in a square root, we are talking about the length of the vector. The code below should give more context.
// This function will return the value of t
// if it returns negative, no collision!
float Raycast01(Ray ray, Sphere sphere) {
Vector3 p0 = ray.Position;
Vector3 d = ray.Normal;
Vector3 c = sphere.Position;
float r = sphere.Radius;
Vector3 e = c - p0;
// Using Length here would cause floating point error to creep in
float Esq = Vector3.LengthSquared(e);
float a = Vector3.Dot(e, d);
float b = Sqrt(Esq - (a * a));
float f = Sqrt((r * r) - (b * b));
// No collision
if (r * r - Esq + a * a < 0f) {
return -1; // -1 is invalid.
}
// Ray is inside
else if (Esq < r * r) {
return a + f; // Just reverse direction
}
// else Normal intersection
return = a - f;
}
On Your Own
Add the following function to the Collisions class:
// TODO: Implement this function
static bool Raycast(Ray ray, Sphere sphere, out float t)
// I've implemented these for you!
// Conveniance method, returns t without an out param
// If no collision happened, will return -1
static float Raycast(Ray ray, Sphere sphere) {
float t = -1;
if (!Raycast(ray, sphere, out t)) {
return -1;
}
return t;
}
// Conveniance method, returns the point of intersection
// instead of p
static bool Raycast(Ray ray, Sphere sphere, out Point p) {
float t = -1;
bool result = Raycast(ray, sphere, out t);
p = new Point(ray.Position.ToVector() + ray.Normal * t);
return result;
}
And provide an implementation for it!
Unit Test
You can Download the samples for this chapter to see if your result looks like the unit test.
The unit test looks visually messy. 3 red spheres are rendered, and a bunch of green lines. Any collision point between a ray and a sphere is marked as blue.
Not every ray is tested against every line, that's why visually this one is impossible to call. The constructor however, will throw errors where needed.
using OpenTK.Graphics.OpenGL;
using Math_Implementation;
using CollisionDetectionSelector.Primitives;
namespace CollisionDetectionSelector.Samples {
class RaycastSphere : Application {
public class Touple {
public Ray ray;
public Sphere sphere;
public bool result;
public Touple(float rayX, float rayY, float rayZ, float normX, float normY, float normZ,
float sphereX, float sphereY, float sphereZ, float rad, bool res) {
ray = new Ray(new Point(rayX, rayY, rayZ), new Vector3(normX, normY, normZ));
sphere = new Sphere(new Point(sphereX, sphereY, sphereZ), rad);
result = res;
}
}
Touple[] touples = new Touple[] {
new Touple(-2, 1, 0, 2, 0, 0, 2, 0, 0, 2, true),
new Touple(-2, 0, 0, 2, 0, 0, 2, 2, 0, 2, true),
new Touple(-2, 0, 0, 2, 0, 0, 0, 0, 0, 2, true),
new Touple(-2, 2, 0, 2, -1, 2, 0, 0, 0, 2, true),
new Touple(2, 1, 0, 2, 0, 0, 2, 0, 0, 2, true),
new Touple(-2, 1, 0, -1, 0, 0, 2, 0, 0, 2, false),
new Touple(-5, 1, 0, 2, 0.4f, 0, 2, 0, 0, 2, false)
};
public override void Intialize(int width, int height) {
GL.Enable(EnableCap.DepthTest);
GL.PointSize(5f);
GL.Enable(EnableCap.CullFace);
GL.PolygonMode(MaterialFace.FrontAndBack, PolygonMode.Line);
foreach(Touple touple in touples) {
float t = 0f;
if (Collisions.Raycast(touple.ray, touple.sphere, out t) != touple.result) {
LogError("Expected ray: " + touple.ray + "\nTo " +
(touple.result ? "intersect" : "not intersect")
+ " sphere: " + touple.sphere);
}
}
}
public override void Render() {
//GL.Enable(EnableCap.CullFace);
GL.PolygonMode(MaterialFace.FrontAndBack, PolygonMode.Line);
base.Render();
DrawOrigin();
GL.Color3(1f, 0f, 0f);
for (int i = 0; i < 3; ++i) {
touples[i].sphere.Render();
}
GL.Color3(0f, 1f, 0f);
foreach (Touple touple in touples) {
touple.ray.Render();
if (touple.result) {
Point p = new Point();
Collisions.Raycast(touple.ray, touple.sphere, out p);
GL.Color3(0f, 0f, 1f);
p.Render();
GL.Color3(0f, 1f, 0f);
}
}
}
private void Log(string s) {
System.Console.WriteLine(s);
}
}
}