Point on line

In order to determine if a point is on a line or not we need to know the slope intercept form of a line. That is, we need to express the line as the equation:

y = m * x + b

Im this equation m and b will be given. We plug in the X and Y position of the point being tested, if the result of the equation is true, the point will be on the line!

However, we express lines by two points, a start point and an end point. Not in slope intercept form. So we have to convert our line into said form.

m in the above equation is the slope of the line, slope is defined as rise over run, or rise / run; that is, the y of the line divided by it's x. So if we convert the line to a vector (end - start), then the slope is said vectors y divided by it's x.

M = (line.end.y - line.start.y) / (line.end.x - line.start.x);

b is the y-intercept. That is, it's the x value of the line where it crosses the y axis. We can find this with our slope, by subtracting the slope from the starting points y and multiplying it by the x value of the point

b = line.start.y - M * line.start.x;

If any of that is unclear, i suggest watching this khan academy video

The algorithm

Now that we can express a line in y intercept form, we can write some code to test if a point is on a line:

bool IsPointOnLine(Line line, Point point)  {
   float m = (line.end.y - line.start.y) / (line.end.x - line.start.x);
   float b = line.start.y - m * line.start.x;

   // At this point, evaluating the equation should be:
   // return point.y == m * point.x + b;
   // But that won't work, because we're working with floats
   // floating point error can accumulate, we have to use an epsilon

   // using an epislon, we can compare the distance of the 
   // equations result to 0 by the epsilon
   if (ABS(point.y - (m * point.x + b)) < EPSILON) {
       return true;
   }
   return false;

   // EPSILON is just a small number, like 0.001f;
}

On Your Own

Add the following function to the Collisions class:

public static bool PointOnLine(Point point, Line line);

And provide an implementation for it!

Unit Test

You can Download the samples for this chapter to see if your result looks like the unit test.

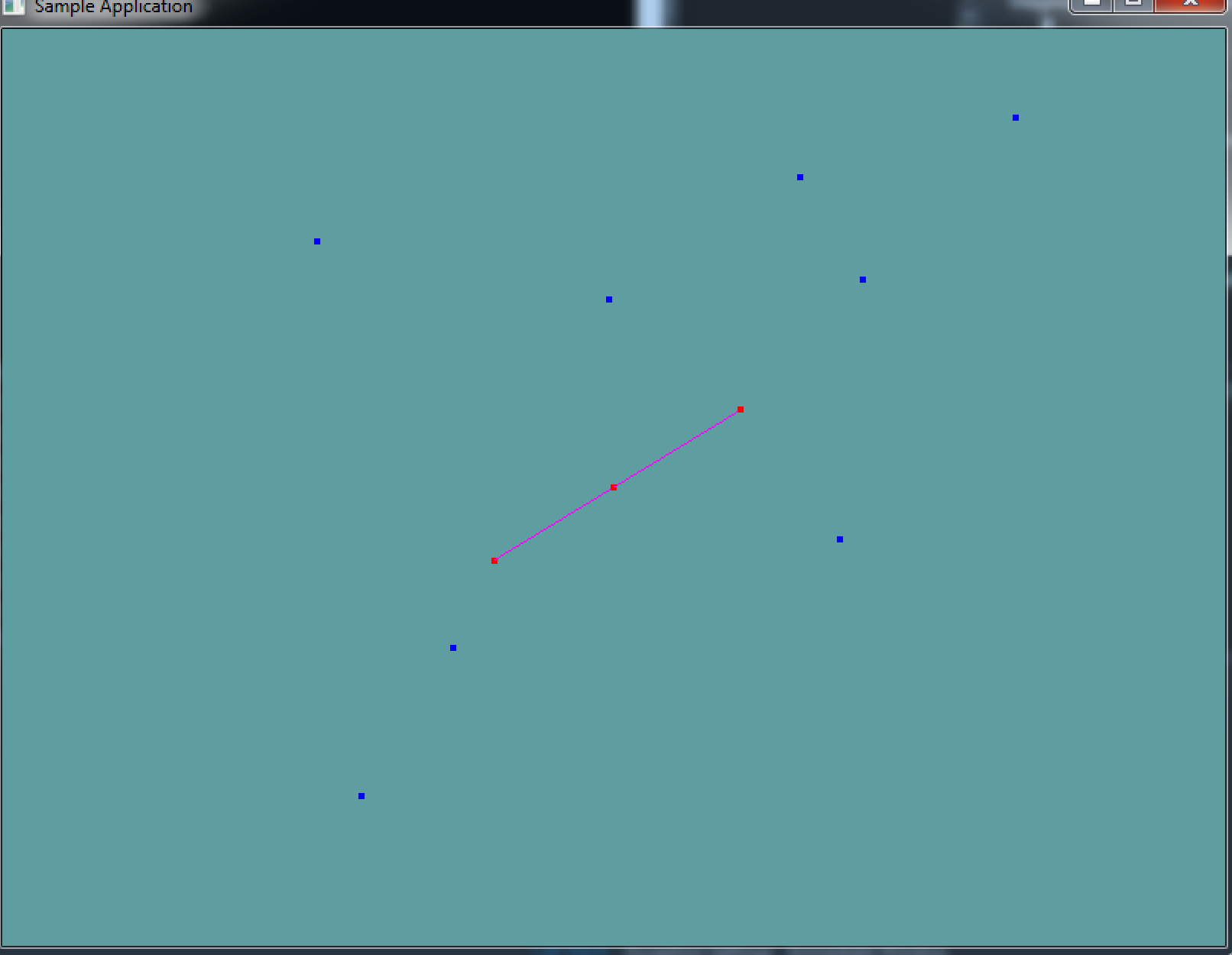
The constructor of this code will spit out errors if they are present. A line is rendered, along with a random sampling of points. Any point that falls on the line is rendered in red, points not on the line are rendered in blue.

using OpenTK.Graphics.OpenGL;
using Math_Implementation;
using CollisionDetectionSelector.Primitives;

namespace CollisionDetectionSelector.Samples {
    class PointOnLine : Application {
        protected Vector3 cameraAngle = new Vector3(120.0f, -10f, 20.0f);
        protected float rads = (float)(System.Math.PI / 180.0f);

        Line testLine = new Line(new Point(-3, -2, -1), new Point(3, 2, 1));
        Point[] testPoints = new Point[] {
            new Point(0, 0, 0),
            new Point(-3, -2, -1),
            new Point(3, 2, 1),
            new Point(7, -2, -1),
            new Point(-4, -7, -8),
            new Point(7, 8, 5),
            new Point(1, 5, -5),
            new Point(-6, 5, 7),
            new Point(1, 6, 8),
            new Point(-7, -10, -4),
            new Point(5, 5, 3)
        };

        public override void Intialize(int width, int height) {
            GL.Enable(EnableCap.DepthTest);
            GL.PointSize(4f);

            for (int i = 0; i < 3; ++i) {
                if (!Collisions.PointOnLine(testPoints[i], testLine)) {
                    System.Console.ForegroundColor = System.ConsoleColor.Red;
                    System.Console.WriteLine("Expected point: " + testPoints[i].ToString() + " to be on Line!");
                }
            }

            for (int i = 3; i < testPoints.Length; ++i) {
                if (Collisions.PointOnLine(testPoints[i], testLine)) {
                    System.Console.ForegroundColor = System.ConsoleColor.Red;
                    System.Console.WriteLine("Expected point: " + testPoints[i].ToString() + " to be on Line!");
                }
            }
        }

        public override void Render() {
            Vector3 eyePos = new Vector3();
            eyePos.X = cameraAngle.Z * -(float)System.Math.Sin(cameraAngle.X * rads * (float)System.Math.Cos(cameraAngle.Y * rads));
            eyePos.Y = cameraAngle.Z * -(float)System.Math.Sin(cameraAngle.Y * rads);
            eyePos.Z = -cameraAngle.Z * (float)System.Math.Cos(cameraAngle.X * rads * (float)System.Math.Cos(cameraAngle.Y * rads));

            Matrix4 lookAt = Matrix4.LookAt(eyePos, new Vector3(0.0f, 0.0f, 0.0f), new Vector3(0.0f, 1.0f, 0.0f));
            GL.LoadMatrix(Matrix4.Transpose(lookAt).Matrix);

            GL.Color3(1f, 0f, 1f);
            testLine.Render();

            foreach (Point point in testPoints) {
                if (Collisions.PointOnLine(point, testLine)) {
                    GL.Color3(1f, 0f, 0f);
                }
                else {
                    GL.Color3(0f, 0f, 1f);
                }
                point.Render();
            }
        }

        public override void Update(float deltaTime) {
            cameraAngle.X += 45.0f * deltaTime;
        }

        public override void Resize(int width, int height) {
            GL.Viewport(0, 0, width, height);
            GL.MatrixMode(MatrixMode.Projection);
            float aspect = (float)width / (float)height;
            Matrix4 perspective = Matrix4.Perspective(60, aspect, 0.01f, 1000.0f);
            GL.LoadMatrix(Matrix4.Transpose(perspective).Matrix);
            GL.MatrixMode(MatrixMode.Modelview);
            GL.LoadIdentity();
        }
    }
}